Parallelization and Analysis of Shortest Path Algorithms
Introduction
A central problem in graph theory is the shortest path problem which is to find the shortest path between two nodes (vertices) in a graph so that the sum of the weight of its constituent edges is minimum. There are four variations of the shortest path problem namely, single-source shortest path (SSSP), breadth-first search (BFS), all-pairs shortest path (APSP), and single-source widest path (SSWP). Many algorithms are in use today which solve this problem. Some of the most popular algorithms are Dijkstra’s algorithm, Bellman-Ford algorithm, A* search algorithm, and Floyd-Warshall algorithm. These algorithms can be applied to undirected as well as directed graphs. Interesting research has been done on this problem due to its many useful real-world applications like road networks, community detection, currency exchange, logistics, electronic design, etc. In this project, we focused on the parallelization of three algorithms - Dijkstra’s algorithm, Bellman-Ford algorithm and Floyd-Warshall algorithm and analyze the speedups against sequential implementations.
Literature Review
Parallelization of the classical shortest path algorithms can be done in several ways. Some of the ways have been discussed by B. Popa et al. [1] Another approach to parallelize Dijkstra’s algorithm has been discussed by A. Crauser et al. [2]
To discuss parallelizing the classical algorithms, we discuss the main idea of the three algorithms we used in our experiment, namely: Dijkstra’s algorithm, Bellman-Ford algorithm and Floyd-Warshall algorithm in the following.
Dijkstra’s algorithm finds the shortest path from a single source and at each step, it finds the minimal distant node, tries to find the shortest paths to other nodes using the recently found shortest node. This algorithm does not consider negative weights and thus cannot be used in a graph with negative weights.
Bellman-Ford algorithm also finds the shortest path from a single source. However, at each step in contrary to Dijkstra’s algorithm, this algorithm updates each node’s distance from the source by the observing the edges. Bellman-Ford algorithm can detect negative weight cycles in a graph and also can be used in a graph with negative weights.
Floyd-Warshall algorithm finds all pair shortest path and does that by observing each node at a time and update paired shortest distances if the node can contribute. This algorithm also can be used in a graph with negative weights.
The pseudocodes of Dijkstra’s algorithm, Bellman-Ford algorithm and Floyd-Warshall algorithm are given in Figure 1 below. Figure 1. Pseudocode of Dijkstra’s algorithm, Bellman-Ford algorithm and Floyd-Warshall algorithm
Figure 1. Pseudocode of Dijkstra’s algorithm, Bellman-Ford algorithm and Floyd-Warshall algorithm
The running time and space complexity of the algorithms are given in Table 1 below:
| ALGORITHM | Time Complexity | Space Complexity |
|---|---|---|
| Dijkstra | $O(V^2)$ | $O(V^2)$ |
| Bellman-Ford | $O(VE)$ | $O(V^2)$ |
| Floyd-Warshall | $O(V^3)$ | $O(V^3)$ |
Our Solution
The three algorithms we chose for our experiment are classic and they have been used in numerous applications. If we observe the time complexity of the algorithms, we see all three are having significant calculation part i.e. arithmetic integrity. According to the roofline model, the more arithmetic intensity an algorithm has, the more performance gain can be achieved using parallelization while increasing the data set. Therefore, we used parallelization to gain performance. For parallelization we used OpenMP.
OpenMP is an API for writing multi-threaded applications. The API supports C/C++ and Fortran on a wide variety of architectures. OpenMP provides a portable, scalable model for developers of shared memory parallel applications.
OpenMP is an abbreviation for Open Multi-Processing. It is comprised of three primary API components:
- Compiler Directives
- Runtime Library Routines
- Environment Variables
OpenMP uses the fork-join model of parallel execution. All OpenMP programs begin as a single process: the master thread. The master thread executes sequentially until the first parallel region construct is encountered. The master thread then creates a team of parallel threads. The statements in the program that are enclosed by the parallel region construct are then executed in parallel among the various team threads. When the team threads complete the statements in the parallel region construct, they synchronize and terminate, leaving only the master thread. The number of parallel regions and the threads that comprise them are arbitrary.
Because OpenMP (Fig. 2) is a shared memory programming model, most data within a parallel region is shared by default. OpenMP provides a way for the programmer to explicitly specify how data is “scoped” if the default shared scoping is not desired.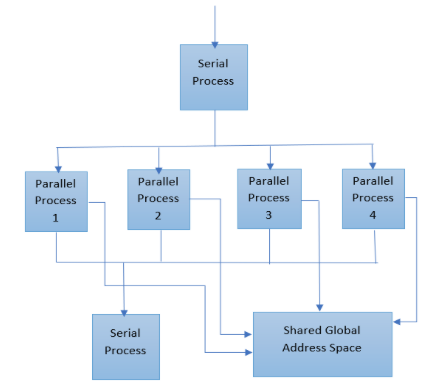 Figure 2. OpenMP thread Model
Figure 2. OpenMP thread Model
Experimental Setup
For the experimental setup, we used four machines. Three of the machines were personal laptops. The fourth one is a computer node of Farber cluster which is the University of Delaware’s second Community Cluster. Farber cluster uses distributed-memory running on Linux operating system (Cent OS). A summary of these machines can be seen in the following table.
| Machine # | Operating System | Architecture | # cores | # threads | RAM (GB) | frequency (GHz) | Compiler |
|---|---|---|---|---|---|---|---|
| 1 (laptop) | OS X | Intel Core i5 3210M | 2 | 4 | 8 | 2.5 | Clang |
| 2 (laptop) | Windows | Intel Core i7 7500U | 2 | 4 | 8 | 2.7 | OpenMP for Visual Studio 2015 |
| 3 (laptop) | Ubuntu | Intel Core i7 8550U | 4 | 8 | 16 | 1.8 | GCC |
| 4 (farber cluster) | Cent OS | Intel(R) Xeon(R) E5-2670 | 20 | 20 | 125 | 2.5 | GCC/ICC(intel) |
To see the compiler effect, we compile the performance using two different compilers: GCC and ICC (intel compiler), both of which are available on Farber.
The data sets used in our project are fake maps generated with script containing different number of nodes. We chose the number node to be 20, 100, 500, 1000 to see the effect of map size. For all the running time reported in this project, it is an average of running the same program on the same machine for 5 times.
Results
Serial Running Time
The sequential running time is plotted in Fig. 3. This is the running time of the graph with 1000 nodes on machine 3. From the figure we can see that Floyd Warshall algorithm is the slowest one and scales close to $O(V^3)$. As the nodes increases, Dijkstra’s algorithm is more efficient: $O(V^2)$ becomes smaller than $O(VE)$ as the number of edge gets larger.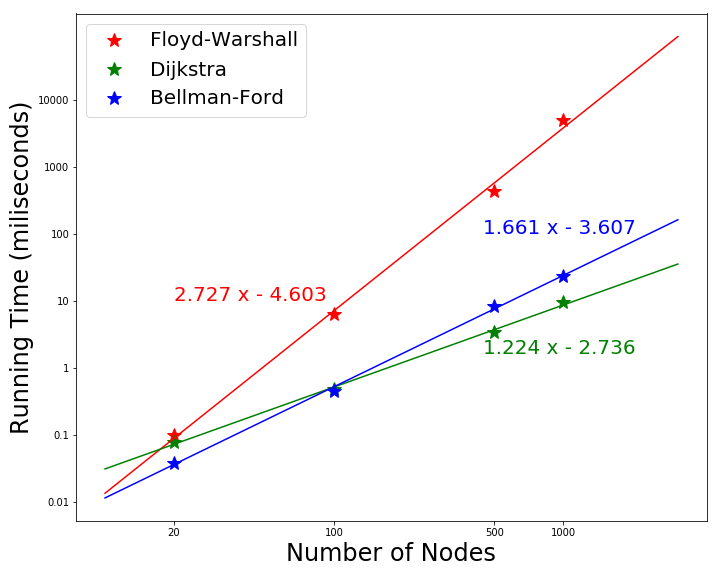 Figure 3. Scale of running time with increasing nodes in the graph
Figure 3. Scale of running time with increasing nodes in the graph
Effects of Compiler: GCC vs. ICC
On farber, we compiled all three algorithms with ICC and GCC. The running time on the 1000 node graph is shown in Fig. 4. The ICC significantly outperformed GCC before we go over 8 threads. For Bellman-Ford and Floyd-Warshall algorithms, the difference is as much as one order in magnitude. This means GCC is not optimized as ICC for the intel CPU. Another interesting result is that the speed up with more threads is more prominent with GCC, as their running time become comparable with 16 threads.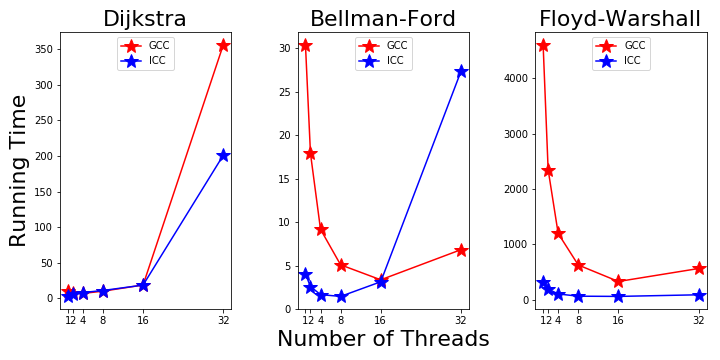 Figure 4. GCC and ICC compiler
Figure 4. GCC and ICC compiler
Parallel Running Time on Machine 1: OS X
On the macbook pro with OS X, we see decreasing running time from 1 to 2 threads. More speed up is achieved with more nodes with parallelization.
For all the three algorithms, there’re no improvement from 2 to 4 threads. This is possibly because it only has 2 physical cores and the 4 logical threads are not so efficient.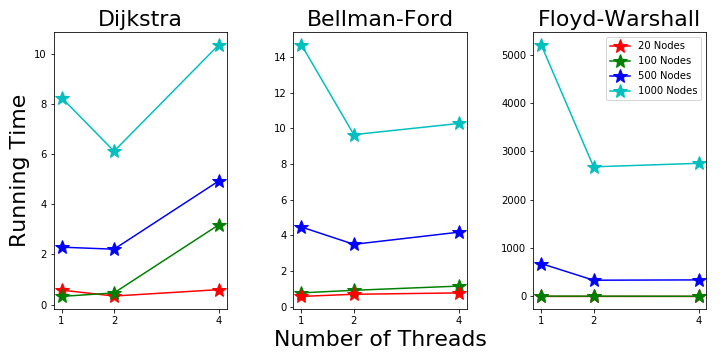 Figure 5. Parallel Running Time on Machine 1
Figure 5. Parallel Running Time on Machine 1
Parallel Running Time on Machine 2: Windows
Machine 2 is a Windows laptop with 2 intel i7 processors and 4 threads. From Fig. 6 we can see Dijkstra’s running time keeps decreasing as more threads are used. The 4 thread mode shows good performance, which is better than the macbook pro.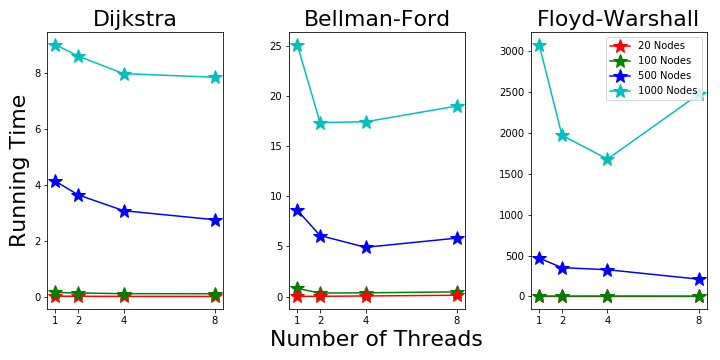 Figure 6. Parallel Running Time on Machine 2
Figure 6. Parallel Running Time on Machine 2
Parallel Running Time on Machine 3: Ubuntu
Machine 3 has 4 physical cores and 8 total threads. The results in Fig. 7 show good speed up going from 1 to 4 threads. However, the 8 threads mode is not very helpful.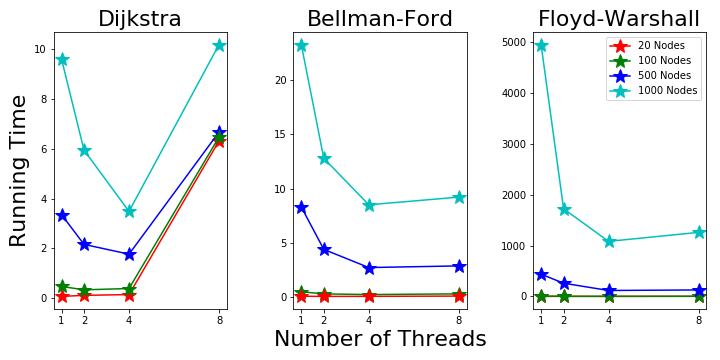 Figure 7. Parallel Running Time on Machine 3
Figure 7. Parallel Running Time on Machine 3
Parallel Running Time on Machine 4: Cent OS
The personal laptops have limited number of CPU cores. But for Farber clusters, it has 20 cores each node, making it good to explore the speed up with more cores. So on machine 4 we focus on the speed up with more threads and just run the three algorithms on one graph with 1000 nodes. The results running with programs compiled with GCC are plotted in Fig. 8. The Dijkstra’s running time start to increase after 4 threads and goes to very high with 32 threads. Further investigation is needed to find out the reasons. The other two algorithms show decreasing running time up to 16 threads. The 32 threads’ running time start to increase as there’re only 20 physical cores.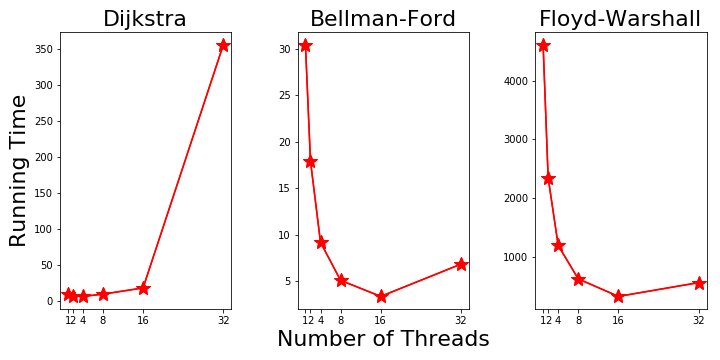 Figure 8. Parallel Running Time on Machine 4
Figure 8. Parallel Running Time on Machine 4
Discussion
Amdahl’s Law and Roofline Model
A general trend in all machines and all algorithms is that ast the number of node increases, the speed up effect becomes more prominent. The average change in running time from one to two threads for graphs with different nodes is shown in Fig. 9. The more nodes in the graph, the more prominence of scale up with more threads. This could be related to Amdahl’s law, which says taht performance improvement to be gained from using some faster mode of execution is limited by the fraction of the time the faster mode can be used. With more nodes in the graph, a larger fraction of the code can be parallelized.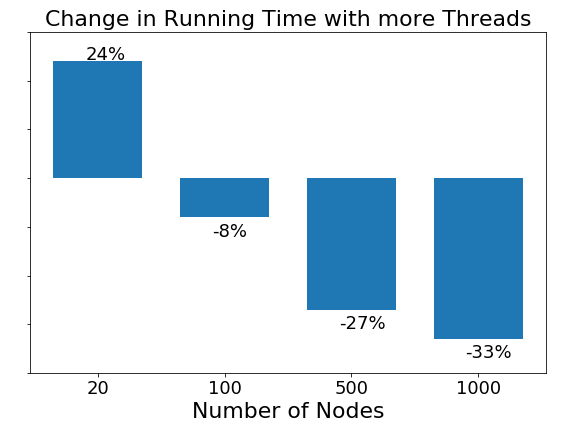 Figure 9. Speed up with respect to graph size
Figure 9. Speed up with respect to graph size
Roofline model tells us that the more arithmetic intensity an algorithm has, the more performance gain can be achieved using parallelization. Arithmetic intensity is the ratio of the total floating point operations to the total data movement. In our problem, the three algorithms has different arithmetic intensity, we would expect different speed up with the three algorithms. Fig. 10 shows the change in running time with different algorithms when going from 1 thread to 2 threads. Floyd-Warshall’s algorithm shows the largest decrease in running time, which is as expected as it has the largest arithmetic intensity with running time scales like $O(v^3)$. Our results correctly demonstrate the Roofline model.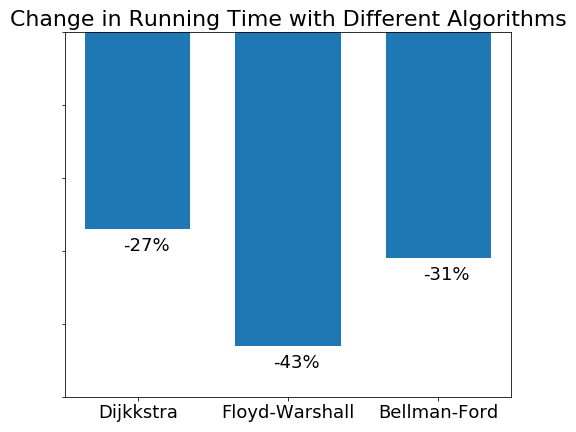 Figure 9 Speed up with respect to different algorithms
Figure 9 Speed up with respect to different algorithms
Applications
There are many applications for shortest path algorithm. To name a few:
- Shortest Path Algorithms are used in google maps to find the short path between the source and destination. We can also say it as it is used to find the direction between two physical locations. Google maps uses A* algorithm to do the same.
- Shortest path algorithm is used in IP routing to find the Open shortest path first.
- It is also used in telephone networks.
- Used to find arbitrage opportunities in currency exchange problem.
Finding Arbitrage Opportunities in Currency Exchange Problem.
For this problem we use Bellman Ford Algorithm. Bellman ford is used because the graph can have negative edges and this algorithm can be used to find if the graph has any negative cycles. For this problem we use negative log of the exchange rates to change as the weights of the edges. This done to change the problem from maximization problem to minimization problem. The Table 4. gives details about the exchange rates between the 6 different currencies. If the graph has any negative cycles indicates that this currency exchange has arbitrage opportunities. We can use backtracking to find between which currency exchange pair this arbitrage opportunity exists. Arbitrage opportunity results from a pricing discrepancy among the different currencies in the foreign exchange market.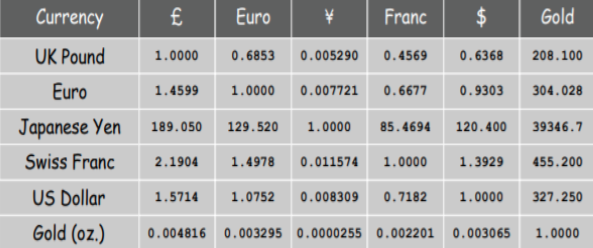
Conclusions
In conclusion, parallelization definitely reduces the time cost compared to the sequential run time of the three algorithms. Doing this project brought into light that the speedup of thread-level parallelization depends on the machine as well as the operating system. The results produced demonstrates Amdahl’s law and the Roofline model. Not only were the benefits of parallelization exposed but to see the algorithms being applied to a useful application like currency exchange was quite interesting.
Future Work
Further investigation can be done on the parallelization of Dijkstra’s algorithm and seek to improve the runtime for more number of threads. It would also be fascinating to apply these effective algorithms for more applications like the GPS system, electronic design, telephone networks, etc. The shortest path problem is certainly worth exploring due to its countless implementations.
All the code and data sets can be found in the GitHub repository as listed in [9].
References
[1]. Popa, B., & Popescu, D. (2016, May). Analysis of algorithms for shortest path problem in parallel. In Carpathian Control Conference (ICCC), 2016 17th International (pp. 613-617). IEEE.
[2]. Crauser, A., Mehlhorn, K., Meyer, U., & Sanders, P. (1998, August). A parallelization of Dijkstra’s shortest path algorithm. In International Symposium on Mathematical Foundations of Computer Science (pp. 722-731). Springer, Berlin, Heidelberg.
[3]. Bellman-Ford algorithm in Parallel and Serial - GitHub link
https://github.com/sunnlo/BellmanFord
[4]. Dijkstra’s Shortest Path Algorithm
https://people.sc.fsu.edu/~jburkardt/cpp_src/dijkstra/dijkstra.cpp
[5]. Floyd, R. W. (1962). Algorithm 97: shortest path. Communications of the ACM, 5(6), 345.
[6]. Floyd Warshall Algorithm
https://engineering.purdue.edu/~eigenman/ECE563/ProjectPresentations/ParallelAll-PointsShortestPaths.pdf
[7]. Bellman-Ford Algorithm Tutorial
https://www.programiz.com/dsa/bellman-ford-algorithm
[8]. Shortest Path Algorithms Tutorial https://www.hackerearth.com/practice/algorithms/graphs/shortest-path-algorithms/tutorial